Optimal Experimental Design of Time Series Data in a Consistent Bayesian Framework

Abstract

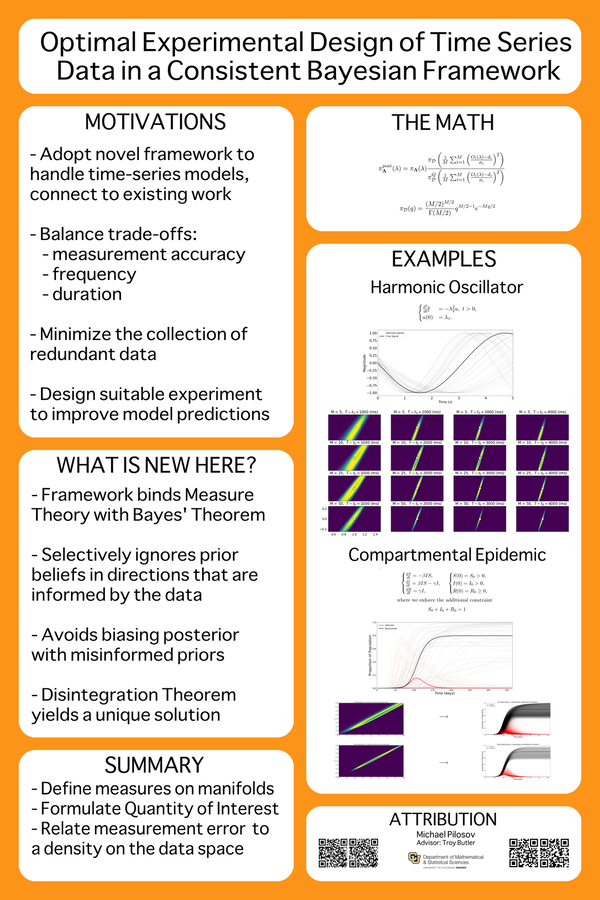
To quantify uncertainties of inputs to models of dynamical systems, a fixed spatial configuration of sensors is often designed and deployed to collect time-series data for solving stochastic inverse problems. A general goal is to configure the sensors so that they provide useful information for the stochastic inverse problem over the full duration of the experiment and provide us with minimally redundant data. We use a recently developed Consistent Bayesian framework for formulating and solving stochastic inverse problems to investigate several design criteria and objectives for deploying sensors. We draw comparisons to other approaches and results based on more classical statistical Bayesian formulations.

see all